FIS structure

The FIS handled by the function library are MIMO type FIS, Multiple Input Multiple Output. The FIS is built by using the information of the configuration file. The basic module contains two main functions, defined within the FIS class: Infer and Performance.

The Infer function infers a value for each active output from the input values. Fuzzy inference obeys the following steps:

1. Fuzzification: done within the INPUT class. For a given input value, the GetDegs function fills the Mfdeg array with the membership values to each input fuzzy set. This array is public.

2. Inference: Each rule conclusion is weighted with the item matching degree for the rule. The rules have the following structure (for a two input one output FIS):

   IF Input 1 is MF 2 AND Input 2 is MF 1 THEN Output 1 is Value 1

   (crisp output)

   IF Input 1 is MF 1 AND Input 2 is MF 1 THEN Output 1 is MF 2

   (fuzzy output)

   
   The ExecRule function of the RULE class calculates the matching degree of the item to the rule, also called rule weight. The calculation is done within the PREMISE class. It uses a conjunction operator between the fuzzy sets in the rule premises for the input variables (Input 1 and Input 2). These fuzzy sets are described by the number 2 and number 1 membership functions for the first rule, 1 and 1 membership functions for the second one). The PREMISE class includes a pointer on the input variable array, which gives it access to the Mfdeg field for each input. The rule matching degree is stored in the public variable Weight within the RULE class. When expert weigts are set (see section FIS menu- Rule window), the rule matching degree is multiplied by the expert weight.

3. Inferred value computation: This computation is handled by FISOUT class. It consists of two main steps.
   • Rule aggregation: Once all the rules have been fired, two options are available to aggregate the rule conclusions: max or sum.

     The rule conclusions are numerical values for a crisp output, or MF labels for a fuzzy output. They constitute a set of possible values.

     The resulting levels are stored into the MuInfer array, the RuleInfer one contains the number of the rule corresponding to the maximum, in case of max aggregation, or the last rule number whose degree has been added, in the sum aggregation case. Both operators can be used with crisp or fuzzy output.

     Note :

     $r$ the number of fuzzy rules, $w^r(x)$ the $rth$ rule matching degree for the multidimensional vector $x$.

     $m$ the number of output MFs (fuzzy output) or the number of distinct rule conclusion values (crisp output).

     $C^r$ the conclusion of the $r{th}$ rule.

     The activation levels after aggregation are the following:

     • max: $$\forall j =1,\ldots,m$$
       $\qquad W^j = \left \{ \underset{r}{max} \left( w^r(x) \right) \vert C^r = j \right \}$

     • sum:
       • crisp output $$\forall j =1,\ldots,m$$
         $\qquad W^j = \sum\limits_r \left( w^r(x) \right) \vert C^r = j$
       • fuzzy output $$\forall j =1,\ldots,m$$
         $\qquad W^j = min \left ( 1, \left \{ \sum\limits_r \left( w^r(x) \right) \vert C^r = j \right \} \right )$

   • Defuzzification: This operation uses aggregation results. The inferred value, $\widehat y_i$ for the $i_{th}$ example, depends on the output nature and its defuzzification operators.
     • crisp output
       1. sugeno operator

          $$\widehat y_i=\frac{\sum\limits_{j=1}^{m}{W^j C^j}}{\sum\limits_{j=1}^{m}{W^j}}$$ (2)

          
          

       2. max crisp operator

          $$\widehat y_i=\left \{ j={argmax} \left( W^j \right) \vert j=1\ldots m \right \}$$

          
          

     • fuzzy output

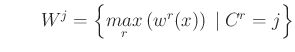
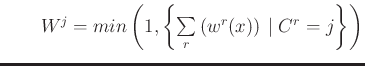
       Figure 5 illustrates the defuzzification possibilities for a fuzzy output.

       Figure 5: Defuzzification

       
       1. weighted area This operator favors the interpolation between linguistic labels. The inferred output is:

          $$\widehat y_i=\frac{\sum\limits_{j=1}^{m}{\alpha}^{C^j} area(C_{\alpha}^j)}{\sum\limits_{j=1}^{m}area(C_{\alpha}^j)}$$ (3)

          
          
          where $m$ is the number of MFs in the partition, $\alpha = W^j$ is the activation level for the $j_{th}$ MF, ${\alpha}^{C^j}$ is the centroid abscissa of $C_{\alpha}^j$, and $C_{\alpha}^j$ a new MF, defined from $C^j$ as follows:
          $$\mu^{C_{\alpha}^j}(x_i)= \left\{\begin{array}{cl} \mu(x_i) & \qquad if \mu^{C^j}(x_i) \le \alpha\\ \alpha & \qquad sinon \end{array}\right.$$

       2. average of maxima The output is $\widehat y_i= mm$ (figure 5). Only the segment corresponding to the maximum activation level is considered, which means the operator mainly operates within one linguistic label.

       3. sugeno It is the same formula as for a crisp output (equation 2), but $C^j$ now represents the middle of the $j_{th}$ MF kernel.

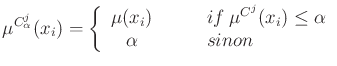
Implication operators

For implicative outputs, three implication operators are available :

• Resher-Gaines : $$\displaystyle a \to b = \left\lbrace \begin{array}{l l} 1 & \qquad si a \le b \\ 0 & \qquad sinon \end{array}\right.$$
• Goguen : $$\displaystyle a \to b = \left\lbrace \begin{array}{l l} 1 & \... ...a = 0 \\ min(1, \frac{b}{a}) & \qquad sinon \end{array}\right.$$

• Gödel : $$\displaystyle a \to b = \left\lbrace \begin{array}{l l} 1 & \qquad si a \le b \\ b & \qquad sinon \end{array}\right.$$

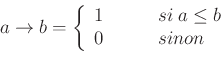
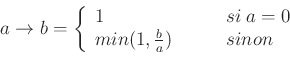
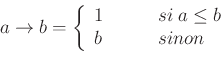
The inference result is a possibility distribution, which may be defuzzified. In the current implementation, no choice is available for the defuzzification operator. The default one is the Mean of maxima, which corresponds to the middle of the distribution kernel.