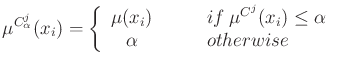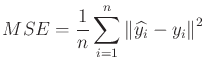Next: Bibliography Up: Starting with FisPro Previous: View the inference results Contents
Figure 10 shows a triangle membership function.
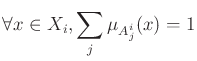 .
.
where
![]() are fuzzy sets defining the iput and output space partitioning.
are fuzzy sets defining the iput and output space partitioning.
Rule aggregation is done in a disjunctive way, meaning that each rule opens a possible range for the output. The two main operators are the maximun and the sum. The resulting levels are, ![]() being the number of rules and
being the number of rules and ![]() the number of labels in the output partition:
the number of labels in the output partition:
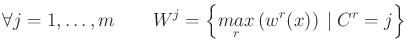
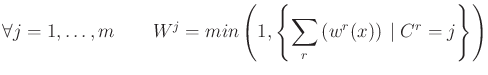
Several defuzzification operators are available. Figure 12 illustrates the process, when two labels have a non null resulting level, for two main kinds of operators.
The inferred system output for the ![]() example is noted
example is noted
![]() .
.
The mean of maxima operator yields
![]() . This operator only considers the segment defined by the maximum level. It mainly works within a single linguistic label. Others similar outputs are possible, for example the minimum value of the maximum level or the maximum one.
. This operator only considers the segment defined by the maximum level. It mainly works within a single linguistic label. Others similar outputs are possible, for example the minimum value of the maximum level or the maximum one.
The weighted area technique favors interpolation between linguistic terms. The output is equal to: