Linguistic variable and fuzzy inference system

• fuzzy set : A fuzzy set is defined by its membership function. A point in the universe, $x$, belongs to a fuzzy set, $A$ with a membership degree, $0 \le \mu_A(x) \le 1$.

  
  Figure 7 shows a triangle membership function.

  Figure 7: A triangle membership function

  

  
  

• Fuzzy set support: the set of real values for which the membership degree is greater then zero, $S_A=\{x \vert \mu_A(x) > 0\}$

  
  

• Fuzzy set kernel: the set of real values for which the membership degree is equal to 1, $K_A=\{x \vert \mu_A(x) = 1\}$

• Fuzzy set prototype: a point is a fuzzy set prototype if its membership degree is equal to 1.

  
  

• Partitioning: Partitioning defines the fuzzy sets for a given variable range. These sets are denoted $A_1$, $A_2$, ...

  
  

• Standardized fuzzy partition: a fuzzy partition of the $X_i$ variable is called a standardized fuzzy partition if $$\forall x \in X_i, \sum_j \mu_{A_j^i} (x) = 1$$.

  Figure 8: Example of a standardized fuzzy partition

  

  
  

• Linguistic variable: In a standard fuzzy partition, each fuzzy set corresponds to a linguistic concept, for instance Very low, Low, Average, High, Very High. During reasoning the variables are referred to by the linguistic terms so defined, and the fuzzy sets determine the correspondence with the numerical values.

  
  

• Fuzzy rule: A fuzzy rule is written as If situation Then conclusion. The situation, called rule premise or antecedent, is defined as a combination of relations such as $x is A$ for each component of the input vector. The conclusion part is called consequence or conclusion.

• Operators:
  • $IS$ : the relation $x is A$ is quantified by the membership degree of $x$ to the fuzzy set $A$.

  • $AND$ : conjunction operator, denoted $\wedge$, the most common operators are minimum and product.

  • $OR$ : disjunction operator, the most common are maximum and sum.

  
  

• Incomplete rule: A fuzzy rule is said to be incomplete if its premise is defined by a subset of the input variables. For instance, the rule

  $$IF x_2 is A_2^1 THEN y is C_2$$

  
  
  is an incomplete rule, as the variable $x_1$ does not appear in its premise. Expert rules are generally incomplete rules. Formally an incomplete rule can be rewritten as an implicit combination of logical connectors $AND$ and $OR$ operating on all the variables. If the universe of the variable $x_1$ is split into three fuzzy sets, the above rule can also be written as:
  $IF \left(x_1 is A_1^1 OR x_1 is A_1^2 OR x_1 is A_1^3 \right) AND x_2 is A_2^1 THEN y is C_2$.

  
  

• Item : an item or individual is composed of a p-dimensional input vector $x$, and eventually of a q-dimensional output vector.

  
  

• Matching degree: For a given data item and a given rule, the rule matching degree, or weight, is denoted $w$. It is obtained by the conjunction of the premise elements: $w=\mu_{A_1^i}(x_1)\wedge \mu_{A_2^i}(x_2) \wedge \ldots \wedge \mu_{A_p^i}(x_p)$, where $\mu_{A_j^i}(x_j)$ is the membership degree of the $x_j$ value to the fuzzy set $A_j^i$.

  
  

• Activation: An item is said to activate a rule, if the rule matching degree for the item is greater than zero.
• Blank threshold: An example is said to be blank or inactive if its maximum matching degree over the rule base is smaller than a threshold value, called blank threshold.

  
  

• Rule prototype: an item is a rule prototype if the rule matching degree for this item is equal to 1, i.e. if example values are proptypes of the premise MFs.

  
  

• Fuzzy inference system (FIS): A fuzzy inference system is composed of three blocks, as shown in Figure 9. The first block is the fuzzification block. It transforms numerical values into membership degrees to the different fuzzy sets of the partition. The second block is the inference engine, with the rule base. The third one implements the defuzzification stage if necessary. It yields a crisp value from the rule aggregation result.

  Figure 9: A fuzzy inference system

  

  
  

• System inferred output: denoted $\widehat{y_i}$ for the $i_{th}$ item. The inferred value, for a given input, depends both on the rule aggregation and the defuzzification operators.

  
  

• The rules If x is A then y is C are of two types:
  1. Conjunctive rules: In this case the rule represents positive knowledge, inputs (A) and output (C) represent pairs of conjunctly possible values. The rule semantic is: If Input is of type A Then a possible output value is C. The rule relationship between inputs and outputs is modelled by a conjunction (t-norm). These rules are inspired from the data base paradigm it is possible because it has been observed, and implement reasoning through similarities. The inferred output is a guaranteed possibility distribution.

  2. Implicative rules: The rule represents negative knowledge and its semantic becomes: If Input is of type A Then Output must be in C. This more formal expression is issued from the Logic research branch of Artificial Intelligence and Computer Science. Instead of cumulating possible values, it works by successive elimination, and removes all values that do not satisfy the rule constraints. The rule relationship between inputs and outputs is modelled by an implication, which may or may not be fuzzy. The inferred output is a (usual) potential possibility distribution. For an expert, the passage from positive to negative knowledge requires a modelling step.

  For a detailed comparison between conjunctive and implicative rules, please refer to [13].

  
  

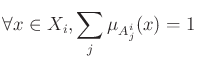• Inference mechanisms: two different ones are necessary:
  1. FITA : First Infer Then Aggregate. It allows inferring a conclusion for each rule separately before aggregating these conclusions. It is used for conjunctive rules, and for implicative ones with precise input data.

  2. FATI : First Aggregate Then Infer. In this case all rules (constraints) are aggregated before inferring the output possibility distribution. Much more difficult to implement, this method is required for implicative rules, as soon as at least one input value is imprecise.