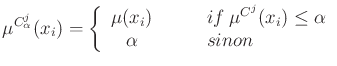Conjonctive rules

There are two main families of conjunctive fuzzy rules:

1. Mamdani type. The rule conclusion is a fuzzy set.
   The rule is written as:
   

   $$IF x_1 is A_1^i AND x_2 is A_2^i \ldots AND x_p is A_p^i$$

   $$THEN y_1 is C_1^i \ldots AND y_q is C_q^i$$

   
   

   where $A_j^i and C_j^i$ are fuzzy sets defining the input and output space partitioning.

   
   

2. Takagi-Sugeno type. The rule conclusion is a crisp value.
   The conclusion of the $i_{th}$ rule for the $j_{th}$ output is calculated as a linear function of the input values: $y_j^i = b_{jo}^i + b_{j1}^i x_1 + b_{j2}^i x_2 + \cdots + b_{jp}^i x_p$, also denoted $y_j^i = f_j^i(x)$.

   In FisPro, for interpretability reasons, the conclusion is limited to a constant $b_{jo}^i$.

• Rule aggregation is done in a disjunctive way for conjunctive rules, meaning that each rule opens a possible range for the output. Two operators are available to aggregate the rule conclusions: max or sum.

  The rule conclusions are numerical values for a crisp output, or MF labels for a fuzzy output. They constitute a set of possible values.

  The resulting levels are stored into the MuInfer array, the RuleInfer one contains the rule number corresponding to the maximum, in case of max aggregation, or the last rule number whose degree has been added, in the sum aggregation case. Both operators can be used with crisp or fuzzy output.

  Note :

  $C r$ the conclusion of the $r{th}$ rule.

  $m$ the number of output MFs (fuzzy output) or the number of distinct rule conclusion values (crisp output).

  The activation levels after aggregation are the following:

  • max: $$\forall j =1,\ldots,m$$
    $\qquad W^j = \left \{ \underset{r}{max} \left( w^r(x) \right) \vert C^r = j \right \}$

  • sum:
    • crisp output $$\forall j =1,\ldots,m$$
      $\qquad W^j = \sum\limits_r \left( w^r(x) \right) \vert C^r = j$
    • fuzzy output $$\forall j =1,\ldots,m$$
      $\qquad W^j = min \left ( 1, \left \{ \sum\limits_r \left( w^r(x) \right) \vert C^r = j \right \} \right )$

• Defuzzification: This operation is required for conjunctive rules and uses aggregation results.

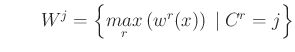
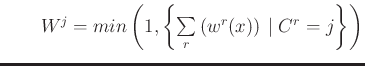
  The inferred value, $\widehat y_i$ for the $i_{th}$ example, depends on the output nature and its defuzzification operators.

  • crisp output
    1. sugeno operator

       $$\widehat y_i=\frac{\sum\limits_{j=1}^{m}{W^j C^j}}{\sum\limits_{j=1}^{m}{W^j}}$$ (4)

       
       

    2. MaxCrisp operator

       $$\widehat y_i=\left \{ j=argmax W^j \left( C^j \right) \vert j=1\ldots m \right \}$$

       
       

  • fuzzy output

    Figure 10 illustrates the defuzzification possibilities for a fuzzy output.

    Figure 10: Defuzzification

    
    1. weighted area This operator favors the interpolation between linguistic labels. The inferred output is:

       $$\widehat y_i=\frac{\sum\limits_{j=1}^{m}{\alpha}^{C^j} area(C_{\alpha}^j)}{\sum\limits_{j=1}^{m}area(C_{\alpha}^j)}$$ (5)

       
       
       where $m$ is the number of MFs in the partition, $\alpha = W^j$ is the activation level for the $j_{th}$ MF, ${\alpha}^{C^j}$ is the centroid abscissa of $C_{\alpha}^j$, and $C_{\alpha}^j$ a new MF, defined from $C^j$ as follows:
       $$\mu^{C_{\alpha}^j}(x_i)= \left\{\begin{array}{cl} \mu(x_i) & \qquad if \mu^{C^j}(x_i) \le \alpha\\ \alpha & \qquad sinon \end{array}\right.$$

    2. average of maxima The output is $\widehat y_i= mm$ (figure 10). Only the segment corresponding to the maximum activation level is considered, which means the operator mainly operates within one linguistic label.

    3. sugeno It is the same formula as for a crisp output (equation 4), but $C^j$ now represents the middle of the $j_{th}$ MF kernel.