Implicative rules

Implicative rule aggregation is conjunctive, because each rule imposes a constraint on the output. The handling of this set of constraints is done using an intersection operator (t-norm). If no rule is active for a given input vector, the output is the universal fuzzy set, meaning that, in case of total ignorance, all output values are equally possible.

Three implication operators are available:

• Resher-Gaines : $$\displaystyle a \to b = \left\lbrace \begin{array}{l l} 1 & \qquad si a \le b \\ 0 & \qquad sinon \end{array}\right.$$

• Goguen : $$\displaystyle a \to b = \left\lbrace \begin{array}{l l} 1 & \... ...a = 0 \\ min(1, \frac{b}{a}) & \qquad sinon \end{array}\right.$$

• Gödel : $$\displaystyle a \to b = \left\lbrace \begin{array}{l l} 1 & \qquad si a \le b \\ b & \qquad sinon \end{array}\right.$$

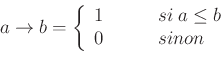
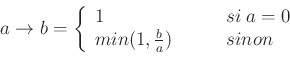
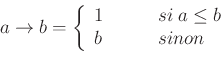
The Resher-Gaines operator is not fuzzy: the possibility distribution corresponds to the kernel of the other two, Goguen and Gödel.

The output partitions must be adapted to the aggregation mode specific to implicative rules. We propose the concept of Quasi standard partition (QSP) as a compromise between interpretability and coherence. Indeed the QSP is derived from a SFP partition, which is well known for its advantages in terms of interpretability. The extra fuzzy sets allow to have a non empty intersection when several rules are simultaneously activated. Figure 11 displays a SFP partition and the equivalent SFP one.

Figure 11: A SFP partition and the QSP equivalent one

Implicative rules offer several advantages compared to conjunctive ones:

• Modus Ponens: The classical version, $A \wedge (A \to C) \models C$, is generalized using fuzzy sets and a fuzzy implication: $A' \wedge ( A \to C ) \models C'$.

• Inferential independence: In the rule base $\{A_j \to C_j, j = 1, \dots, n\}$, The inferred output for $A_i$ is equal to $C_i$, if the rule $A_i \to C_i$ exists, whatever the other rules are.

• Respect imprecision: Because rule accumulation corresponds to eliminating possible output values, the imprecision of the output possibility distribution is meaningful and may be analysed.

  It is also possible to extract a precise value by defuzzification. The current implementation does not allow to parameterize the defuzzification operato. The default one is the Mean of maxima, which corresponds to the middle of the distribution kernel.

• Detect conflicts: An empty output possibility distribution means there is an inconsistency in the rule base, the contraints are not compatible.