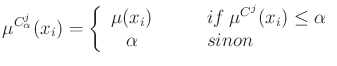suivant: Règles implicatives monter: Petit glossaire de la précédent: Variable linguistique et système Table des matières
Les règles conjonctives sont rassemblées en deux familles :
où
![]() sont des ensembles flous qui définissent le partitionnement des espaces d'entrée et de sortie.
sont des ensembles flous qui définissent le partitionnement des espaces d'entrée et de sortie.
Pour des raisons d'interprétabilité, dans FisPro, la sortie est limitée à une constante au lieu de cette combinaison linéaire des entrées.
Notons :
![]() le nombre de termes linguistiques de la partition de la variable de sortie (sortie floue) ou le nombre de valeurs différentes des conclusions des règles (sortie nette).
le nombre de termes linguistiques de la partition de la variable de sortie (sortie floue) ou le nombre de valeurs différentes des conclusions des règles (sortie nette).
![]() la conclusion de la règle
la conclusion de la règle ![]() .
.
Les niveaux d'activation résultant de l'agrégation sont :
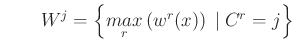
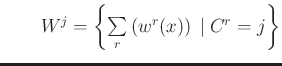
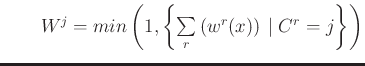
Les opérateurs de défuzzification sont différents selon le type de sortie, nette ou floue.
La figure 10 illustre le processus de défuzzification pour une sortie floue.