suivant: Optimisation monter: Menu Apprentissage précédent: HFP SIF Table des matières
Cette procédure est applicable à n'importe quel système d'inférence floue, spécialement ceux construits par apprentissage.
Le principe consiste à essayer de supprimer des variables dans la définition des règles ainsi que des règles entières. Ces modifications sont acceptées si les indices de performance et de couverture, présentés dans la section 2, restent dans des limites acceptables.
La procédure est réalisée à plusieurs niveaux. Le plus important, effectué dans tous les cas, est celui de la fusion d'un groupe de règles proches au sens de leurs prémisses. Deux autres niveaux sont optionnels : la suppression des règles, et la suppression de variables au sein de chacune des règles.
Paramètres principaux
La simplification s'accompagne généralement d'une perte de performance, celle-ci peut être relative, exprimée en pourcentage de la valeur initiale, ou bien absolue, dans ce cas l'utilisateur indique la limite.
Au cours de l'étape de fusion d'un groupe de règles, la couverture ne
peut qu'augmenter. Il n'en n'est pas de même lors de l'étape
optionnelle d'élimination des règles. La perte de couverture maximale autorisée est fixée par défaut à 10%, et peut être modifiée.
Paramètres secondaires
Comme la suppression de variables de la définition de la règle
correspond à un élargissement de l'espace d'entrée, il est nécessaire
de vérifier que cet élargissement ne conduit pas à des simplifications
abusives. Le seuil d'homogénéité fixe la valeur maximale de la
dispersion des sorties observées des exemples attirés par la règle.
L'indice d'hétérogénéité dépend du type de la sortie. Pour une sortie
continue, il s'exprime comme :
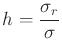 .
. ![]() est l'ensemble des exemples qui
activent le plus la règle,
est l'ensemble des exemples qui
activent le plus la règle, ![]() est l'écart type des sorties
dans
est l'écart type des sorties
dans ![]() pondéré par les degrés de vérité de la règle pour chacun
des exemples,
pondéré par les degrés de vérité de la règle pour chacun
des exemples, ![]() l'écart type dans l'ensemble complet. Pour une
sortie de type classification, il s'agit d'une entropie normalisée par
le logarithme du nombre de classes. Il est surtout significatif pour
les problèmes de classification. Par défaut, nous le rendons inactif
pour les problèmes de regression (valeur 1000) et nous proposons
0.8 pour une sortie de type classification.
l'écart type dans l'ensemble complet. Pour une
sortie de type classification, il s'agit d'une entropie normalisée par
le logarithme du nombre de classes. Il est surtout significatif pour
les problèmes de classification. Par défaut, nous le rendons inactif
pour les problèmes de regression (valeur 1000) et nous proposons
0.8 pour une sortie de type classification.
L'option Garder la dernière règle, activée par défaut,
indique que la procédure ne doit pas supprimer la dernière règle dont
la conclusion correspond à une classe donnée, dans le cas d'une sortie
nette et de l'option classification, ou bien à un sous-ensemble flou
donné pour tout type de sortie floue.
Il est possible de spécifier une fichier de validation. Dans ce cas
il est utilisé à chaque étape pour retenir ou non la simplification calculée
à partir du fichier d'appprentissage.
Résultat
Le résultat de la procédure est résumé dans un fichier, result.simple. Ce fichier ne contient qu'une ligne qui décrit le système simplifié : la première colonne indique le nom du système, celui mentionné dans le fichier de configuration, puis les indices décrits dans la section 2 et enfin les caractéristiques de la base de règles, voir la section 3 :
Une option permet de supprimer l'ensemble des fichiers intermédiaires créés par cette procédure, y compris les fichiers de type SIF.